Phase Space in Relativistic Mechanics

String Theory without the Baggage, Episode 3.

Hey Friends,

So far we’ve been discussing the phase space of point particles. Last time we explored how moving from the nonrelativistic case to the relativistic one is complicated by the mass-shell condition. Today we’re going to explore just how complicated this construction can get. I promise these ideas will be really important in our discussion of relativistic strings.

I’ve also left a question in the notes for you folks - especially any algebraic geometers out there. Let me know what you think!

Sean

---

In Special Relativity, the configuration space of a point particle of mass m is the same. We are still only concerned with R^3. It is the kinetic sector that becomes more complex, as now the momenta must sweep out a hyperboloid, rather than a vector space.

The Mass-Shell Condition and de Sitter Space

Recall that, geometrically, we can think of the nonrelativistic phase space as the vector bundle

\(\mathbb{P} = \mathrm{T}^{\star}\mathbb{R}^{3} \cong \mathbb{R}^{6},\)

where the fibre of the bundle - the space of possible momenta at any given point x in configuration space - is a copy of R^3.

The prescription of Special Relativity is to replace that R^3 fibre with the curved, hyperboloid in R^3,1, defined by

\(\begin{equation}-p^{\mu}p_{\mu} = -E^{2}/c^{2} + p_{x}^{2} + p_{y}^{2} + p_{z}^{2} = -m^{2}c^{2}.\end{equation}\)

Compared to R^6, this relativistic phase space has the potential to be an unintuitive monster:

Relativistic phase space (P) modeled as a bundle over R^3 with the fibre given by the mass-shell constrained hyperboloid discussed last time.

Algebra will save us. The main idea here is that the old, classical fibre, R^3, now parametrizes the new, relativistic one.

This is where some folks will jump in and say things like “well that’s why we use R^3,1, HELLO!!!” or “You really should maintain manifest Lorentz Symmetry if you’re going to work in Special Relativity.”

If you are one of those types, go outside and take a breath. This piece specifically avoids those constructions precisely because they implicitly add other complications. For example, you will have traded a point particle configuration space for one involving worldlines. Sometimes the party line on these issues is overly simplistic¹. There is no “free lunch” here; we’ll get to that treatment next time. The whole point of this episode is to expose the actual complexity of the situation.

Going off the Deep End

Consider SO(3,1), the Lie group of Lorentz transformations of four-dimensional spacetime, and Let 𝔰𝔬(3,1) be it's associated Lie algebra². Being a continuous group with six parameters, SO(3,1) can also be thought of as a six-dimensional curved space. In particular, 𝔰𝔬(3,1) can be thought of as the six-dimensional vector space of infinitesimal group transformations - the vector space of vectors tangent to SO(3,1) at the identity element.

To perform the mapping from classical phase space, discussed here:

Phase Space in Classical Mechanics

to relativistic phase space, we first identify the fiber R^3 with the three-dimensional subspace of 𝔰𝔬(3,1) corresponding to Lorentz boosts:

\(p_x \mapsto \Lambda(v_x),\; p_y \mapsto \Lambda(v_y)\; \mathrm{and}\; p_z \mapsto \Lambda(v_z). \)

Concretely, such a boost rotates energy and momentum:

\(\Lambda(v) : (E,0) \mapsto ( E\gamma , \gamma vE/c^2)\)

where

\(\gamma = \frac{1}{\sqrt{1 - (v/c)^2}}.\)

We then simply employ the standard exponential map to follow those parameters from the Lie algebra into the full Lie Group.

Reimagining the phase space fibre as a submanifold of the Lie group SO(3,1).

Put differently, going from classical to relativistic phase space is a bundle injection Λ:

Given that SO(3,1) looks locally like R^3 - the Lie algebra-as-vector space 𝔰𝔬(3, 1) - we can think of the nonrelativistic phase space cotangent bundle as a being localized fibrewise near the identity element of the boost submanifold of SO(3,1).

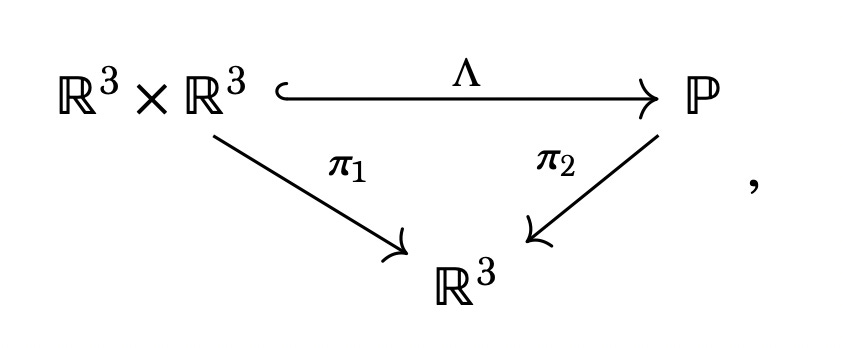
where the nonrelativistic case is identified with a small neighborhood of relatively small velocities near the origin of each fibre.

Putting everything together then, we have a rather wild looking diagram to chase:

A diagrammatic expression of what we’re trying to say in this post, for those of you who think primarily in terms of abstract nonsense.

While at least intuitively interpretable, hopefully this still convinces you that the structure is still a complicated mess!

One reason for this is the nature of the relativistic fibre. While it is a subset - indeed a submanifold - of the Lie Group SO(3,1), it is not a subgroup.

We will return to clarify this idea in a future episode³.

The commutator of two boosts in the Lie algebra 𝔰𝔬(3,1) amounts to a rotation, which means that we cannot algebraically isolate the “boosts” from the “rotations” in the full group. This means that the bundle structure of the relativistic phase space has neither the nice properties a vector bundle nor a principle bundle. It is some awkward intermediate thing.

It is this awkwardness the accounts for the often awkward notations used when first teaching Special Relativity. In practice, we typically try to maintain explicit Lorentz symmetry in our equations - typically at the cost of some implicit constraints or other conditions being carried along for the ride.

Next time, we’ll try to simplify this mess of a phase space by keeping Lorentz covariance manifest.

1. To conjoin a pair of famous Physics aphorisms: “It is important to have has much beauty as possible in one’s equations, but no more than that.”

2. We’ll use a lot of Lie algebra terminology in this series. We put together a series of videos on this topic a while back, starting here. For more color around isometries of R^3,1 specifically, check out our videos on representations of su(2) and sl2(R). If you’d like a really solid introduction from a proper Mathematical, check out Michael Penn’s channel. He just started a series on Lie algebras, specifically.

3. The implications of this point has been giving me some pause. Specifically, I’m concerned about particle orbits in this phase space, subject to some force. Let’s have some discussion around this if you like! Send me a note! The full phase space surely has the capacity to be covariant with respect to a generic SO(3,1) transformation: a rotation can be managed in both the base and the fibre. This sort of forced Terrell Rotation would presumably be required by such particle motion. It is certainly true that a generic choice of momentum vector can be mapped back to a rest frame with a single boost, but a continuous path through them? That should induce some kind of rotation in the base. Would this be interpreted as some kind of torsion? For a visual representation around what I’m talking about, check out MIT’s A Slower Speed of Light.