The Displacement Operator

So ends our mini-Series on Heisenberg algebras in Quantum Mechanics.

Hey Friends,

This post will conclude our discussion of the application of representation theory of Heisenberg algebras to Quantum Mechanics. It was meant as an introduction to the subject - and to bring physicists along for the ride. Our next chapter in this series will bring a bit of formality back to these ideas.

Also. The Substack LaTeX engine on mobile has not being behaving well. Hence the piece might be better viewed on desktop. That said, we’ll try to come back and replace the equations with images to fix any issues we encounter, but it will probably take a few days.

Thanks for reading!

Sean

---

Last time we studied coherent states of Quantum harmonic oscillator. These were representatives of the Hilbert space parametrized by a complex number α:

\(| \alpha \rangle = e^{-\frac{1}{2}|\alpha|^{2}} \sum_{n=0}^{\infty} \frac{1}{n!} \alpha^{n} \, a^{\dagger n} | \varnothing \rangle.\)

Here we have packaged the time dependence implicitly with a phase angle dependent on the angular frequency of the oscillator ω,

\(\alpha = \alpha_{0}e^{-i\omega t}.\)

Our aim today is to show that these states can be generated by an operator

\(D(\alpha) = \exp\left(\alpha a^{\dagger} - \bar{\alpha}a\right),\)

so that

\(| \alpha \rangle = D(\alpha) |\varnothing\rangle.\)

The Baker-Campbell-Hausdorff Formula

Let A be a linear operator on some Hilbert space of physical states. We can define a formal operator, called the exponential of A, by the form series

\(e^{A} = \sum_{n=0}^{\infty} \frac{1}{n!}A^{n}.\)

Infinite sums of operators are tricky to deal with. We need to make sure their action on their respective Hilbert space is well-defined. In particular, when acting upon an eigenvector of the operator A, the sum should converge. Generically, this should be true if A is scaled by a complex number with a sufficiently small modulus.

Let us assume A and B are two operators with well-defined exponentials. You might be curious how to manipulate products of exponentials. In particular, what it the commutator,

\([e^{A},e^{B}] = e^{A}e^{B} - e^{B}e^{A}?\)

The Baker-Campbell-Hausdorff formula gives an algebraic relationship that helps answer this question. Specifically, it gives that

\(e^{A}e^{B} = \exp\left(A + B + \frac{1}{2}[A,B] + \frac{1}{12}[A,[A,B]] - \frac{1}{12}[B,[A,B]] + \cdots \right).\)

The additional terms involve nested commutators of the operators A and B.

For the case of the Heisenberg algebra, this formula is particular simple. In Dirac’s basis,

\([a,a^{\dagger}] = 1.\)

Hence, if the commutator of A and B commutes with both A and B, as with the ladder operators, the Baker-Campbell-Hausdorff formula terminates,

\(e^{A}e^{B} = \exp\left(A + B + \frac{1}{2}[A,B] \right).\)

Additionally, because [A,B] is essentially a constant, we may write

\(e^{A+B} = e^{-\frac{1}{2}[A,B] }e^{A}e^{B}.\)

This is the main formula we shall use today.

That said, we still need to answer our question, what is the commutator of the exponential operators? Applying the definition this is just

\([e^{A},e^{B}] = \exp\left(A + B + \frac{1}{2}[A,B] \right) - \exp\left(A + B - \frac{1}{2}[A,B] \right).\)

Simplifying as above,

\([e^{A},e^{B}] = 2\sinh\left(\frac{[A,B]}{2}\right) \; e^{A+B}.\)

Where the hyperbolic sine function is also just a formal series of operators,

\(\sinh A = \frac{1}{2}\left(e^{A} - e^{-A}\right) = \sum_{n=1}^{\infty} \frac{A^{2n+1}}{(2n+1)!}.\)

The Displacement Operator

For a complex number α, let us take

\(A = \alpha a^{\dagger} \quad \mathrm{and} \quad B = -\alpha^{\star} a.\)

Plugging in to our formula above,

\(\exp\left(\alpha a^{\dagger} - \alpha^{\star}a\right) = \exp\left(-\frac{1}{2}|\alpha|^{2} [a^{\dagger},a]\right)e^{\alpha a^{\dagger}}\exp(\alpha a^{\dagger}) \exp(-\alpha^{\star}a).\)

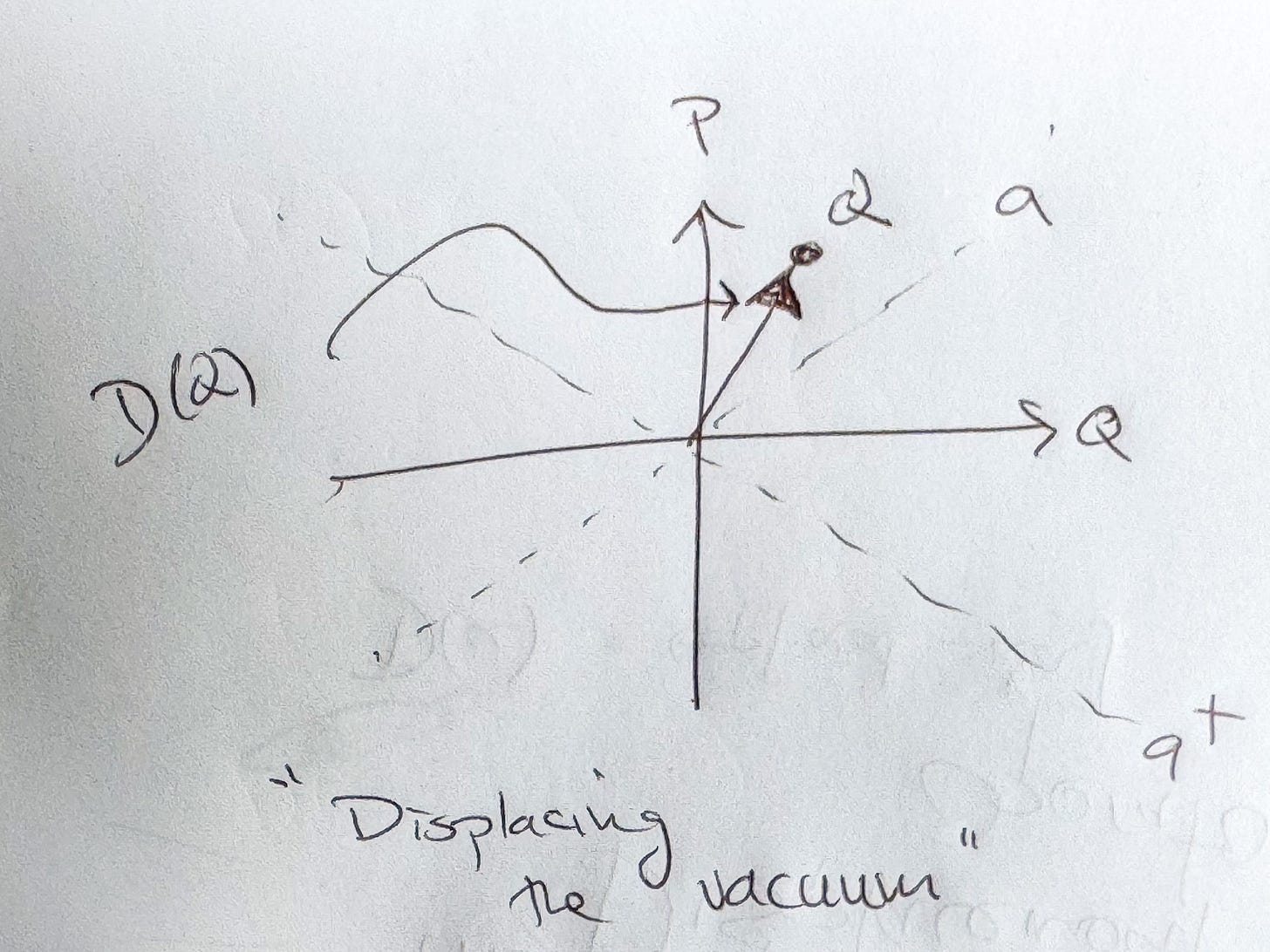
Let us define this as the displacement operator D(α):

\(D(\alpha) = \exp\left(\alpha a^{\dagger} - \alpha^{\star}a\right).\)

Simplifying the commutator algebra, we can write this definitively as,

\(D(\alpha) = e^{-\frac{1}{2}|\alpha|^{2}}e^{\alpha a^{\dagger}}e^{-\alpha^{\star}a}.\)

Let us attempt to act with D(α) on the vacuum.

To that end, first we expand the exponential of α*a,

\(e^{\alpha^{\star}a} = \sum_{n=0}^{\infty} \frac{1}{n!}\alpha^{\star n}a^{n}.\)

Only the first term of this whole series has a nonzero action on the vacuum. Hence,

\(e^{\alpha^{\star}a} |\varnothing\rangle = \sum_{n=0}^{\infty} \frac{1}{n!}\alpha^{\star n}a^{n} |\varnothing\rangle = | \varnothing\rangle.\)

It immediately follows from our discussion last time that, D(α) gives us the coherent state associated with α. Amusingly, the normalization factor falls right out of the algebra! So indeed

\(D(\alpha) | \varnothing\rangle = | \alpha \rangle.\)

The displacement operator D(α) essentially moves the vacuum around in optical / oscillator phase space, taking the ladder operators to span a one, complex dimensional space from which the parameter α is drawn.

The Algebra of Displacement Operators

As with our discussion of the exponential operators, you might wonder about the commutator of two Displacement operators. Let us compute.

\([D(\alpha) , D(\beta) ] = [\exp\left(\alpha a^{\dagger} - \alpha^{\star}a\right),\exp\left(\beta a^{\dagger} - \beta^{\star}a\right)].\)

Because these are both exponential operators, we can once again immediately deploy our formula with

\(A = \alpha a^{\dagger} - \alpha^{\star}a \quad \mathrm{and} \quad B = \beta a^{\dagger} - \beta ^{\star}a.\)

Note that

\([A,B] = \alpha \beta^{\star} - \alpha^{\star}\beta.\)

Applying the formula,

\(D(\alpha)D(\beta) = e^{\frac{1}{2}\left(\alpha\beta^{\star} - \alpha^{\star}\beta\right)}D(\alpha + \beta).\)

As with exponentials, we see that multiplying displacement operators amounts to the addition of complex parameters, together with an intertwining phase.

In particular, we see that the inverse of the displacement operator D(α) is just D(-α),

\(D(\alpha)D(-\alpha) = e^{0}D(0) = 1.\)

The commutator of two displacement operators can also be pulled directly from the formulae above,

\([D(\alpha),D(\beta)] = \left(2\sinh \frac{\alpha \beta^{\star} - \alpha^{\star}\beta}{2}\right) D(\alpha + \beta). \)

Notice that D(α) commutes both with itself and its inverse.

Actually, we can say more. Define λ so that β = λα.

\([D(\alpha),D(\lambda \alpha)] = \left(2\sinh \frac{|\alpha|^{2}}{2}[ \lambda^{\star} - \lambda]\right) D(\alpha + \lambda\alpha). \)

Hence two nontrivial displacement operators commute precisely when their complex parameters differ by a nonzero phase.

The Case of n-harmonic oscillators

This construction carries through immediately for multiple harmonic oscillators. For the case of n-oscillators,

From One Oscillator to Many

we have the displacement operator

\(D(\vec{\alpha}) = \exp\left(\sum_{j=1}^{n}\alpha_{j} a_{j}^{\dagger} - \alpha_{j}^{\star}a_{j}\right).\)

For finite n, the algebra follows exactly. The main difference is we now need n complex numbers, which we can package as a vector in C^n.

We have already seen a that Quantum fields correspond to an infinite set of harmonic oscillators,

Grading the Electromagnetic Field

As we pass to infinite n, convergence becomes an issue. In particular, the Gaussian normalization term becomes

\(\exp\left( -\sum_{j=0}^{\infty} |\alpha_{j}|^{2}\right).\)

We are left with a number of options. First, we could throw up our hands and identify all such coherent states with the vacuum, taking the limit that this factor approaches zero¹.

Second, we could assert that all but a finite number of the complex parameters are zero in a well-defined displacement operator.

Such issues with infinities are the main nuance when studying the vertex operator connections of affine Lie algebras. For the relatively simple case of affine sl2, these vertex operators are constructed following a formula similar to that of our displacement operator.

In string theory, vertex operators correspond to the interaction of physical states from the perspective of the string world sheet. Hence they involve the study of perturbative quantum field theory. To make the leap from Quantum Mechanics to these structures, we’re going to need to learn a bit about Lie algebras. That’s for next time.

This concludes are preliminary discussion of Quantum Mechanics.

1. There are already plenty of infinities to worry about in the study of quantum fields, such as the infinite copies of the zero-point vacuum energy associated with an infinite number of harmonic oscillators.